 +
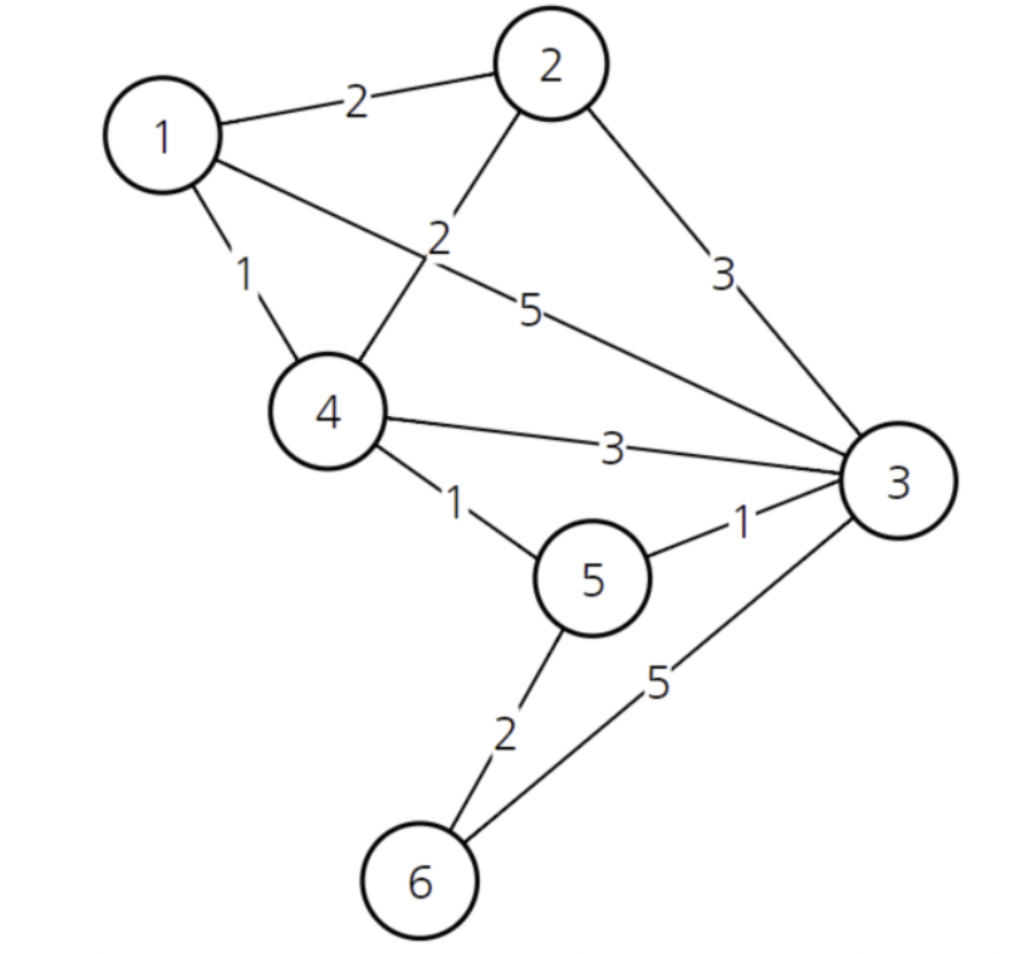
+<특정 노드에서 다른 노드로가는 그래프>
+
+| | 1 | 2 | 3 | 4 | 5 | 6 |
+| --- | --- | --- | --- | --- | --- | --- |
+| 1 | 0 | 2 | 5 | 1 | inf | inf |
+| 2 | 2 | 0 | 3 | 2 | inf | inf |
+| 3 | 5 | 3 | 0 | 3 | 1 | 5 |
+| 4 | 1 | 2 | 3 | 0 | 1 | inf |
+| 5 | inf | inf | 5 | 1 | 0 | 2 |
+| 6 | inf | inf | 5 | inf | 2 | 0 |
+
+
+
+<특정 노드에서 다른 노드로가는 그래프>
+
+| | 1 | 2 | 3 | 4 | 5 | 6 |
+| --- | --- | --- | --- | --- | --- | --- |
+| 1 | 0 | 2 | 5 | 1 | inf | inf |
+| 2 | 2 | 0 | 3 | 2 | inf | inf |
+| 3 | 5 | 3 | 0 | 3 | 1 | 5 |
+| 4 | 1 | 2 | 3 | 0 | 1 | inf |
+| 5 | inf | inf | 5 | 1 | 0 | 2 |
+| 6 | inf | inf | 5 | inf | 2 | 0 |
+
++ +(1번노드 기준 다른 노드로 가는 최단경로 구하기) + +
+ +1. 표에서 1번 노드 기준 5로 가는 최소비용은 inf이지만 4를 거쳐 5로 가는 비용은 2이므로 최소 비용을 갱신 + + + | 0 | 2 | 5 | 1 | 2 | inf | + | --- | --- | --- | --- | --- | --- | +2. 6번 노드 기준 1번으로 가는 최소 비용은 5와4를 거친 비용이므로 최소 비용을 갱신 + + + | 0 | 2 | 5 | 1 | 2 | 4 | + | --- | --- | --- | --- | --- | --- | +3. 1번 노드에서 3번 노드로 가는 최소 비용은 4번 노드와 5번 노드를 거쳐 가는 비용이므로 갱신 + + + | 0 | 2 | 3 | 1 | 2 | 4 | + | --- | --- | --- | --- | --- | --- | +4. 최종 완성 + + + | 0 | 2 | 3 | 1 | 2 | 4 | + | --- | --- | --- | --- | --- | --- | + +
+ +## ****우선순위 큐를 사용하는 다익스트라(Dijkstra) 알고리즘**** + +너비 우선 탐색과 유사한 형태를 가진 알고리즘으로, 너비 우선 탐색처럼 시작점에서 가까운 순서대로 정점을 방문해간다. + +> ⇒ 물론 가중치가 있는 그래프에서는 너비 우선 탐색을 그대로 적용할 순 없기 때문에 우선순위 큐를 사용하여 이를 해결한다. + +
+ +- 다익스트라 알고리즘은 우선순위 큐 + BFS의 형태를 가지고 있다. +- 각 정점까지의 최단 거리를 저장하는 배열 dp[]를 유지하며, 정점을 방문할 때마다 인접한 정점을 모두 검사한다. +- 간선 (u, v)를 검사한다고하면 u까지의 최단 거리에 (u, v)의 가중치를 더해 v까지의 경로의 길이를 찾는다. 만약 이 길이가 최단거리라면 dp[v]를 갱신하고, (v, dp[v])를 큐에 넣는다. + +
+ +<우선순위 큐를 이용한 다익스트라 알고리즘 구현> + +```java +public class DijkstraExample { +static List
+ +## ****플로이드 와샬(Floyd Warshall) 알고리즘**** + +
 +
+- **Floyd Warshall 알고리즘**은 **모든 정점**에서 **다른 모든 정점**으로의 최단 경로를 구하는 알고리즘이다.
+- Floyd Warshall 알고리즘의 핵심 아이디어는 애초에 거쳐가는 정점을 하나씩 다 설정을 하여 직접 확인하는 방법, 즉 **거쳐가는 정점을 기준으로 최단 거리를 구하도록** 구성되어있다.
+- 모든 쌍 간의 최단 거리를 구하고 싶다면 플로이드 와샬 알고리즘을 사용하면 된다.
+
+
+
+
+- **Floyd Warshall 알고리즘**은 **모든 정점**에서 **다른 모든 정점**으로의 최단 경로를 구하는 알고리즘이다.
+- Floyd Warshall 알고리즘의 핵심 아이디어는 애초에 거쳐가는 정점을 하나씩 다 설정을 하여 직접 확인하는 방법, 즉 **거쳐가는 정점을 기준으로 최단 거리를 구하도록** 구성되어있다.
+- 모든 쌍 간의 최단 거리를 구하고 싶다면 플로이드 와샬 알고리즘을 사용하면 된다.
+
+
++ +### 경유점 + +플로이드 알고리즘은 경로의 경유점 개념을 알아야한다. 두 정점 u, v를 잇는 어떤 경로가 있다고 할때 이 경로는 시작점 u와 끝점 v를 가지는 것이다. 이 외에 이 경로는 다른 정점들을 지나쳐 갈 수 도 있다. + +>⇒ u와 v를 직접 연결하는 간선이 없거나, 다른 정점을 경유해서 가는 편이 전체 경로가 더 짧아 질때 이와 같은 경로를 거쳐가는 정점들을 **경유점**이라 한다. + +
 +
+
+
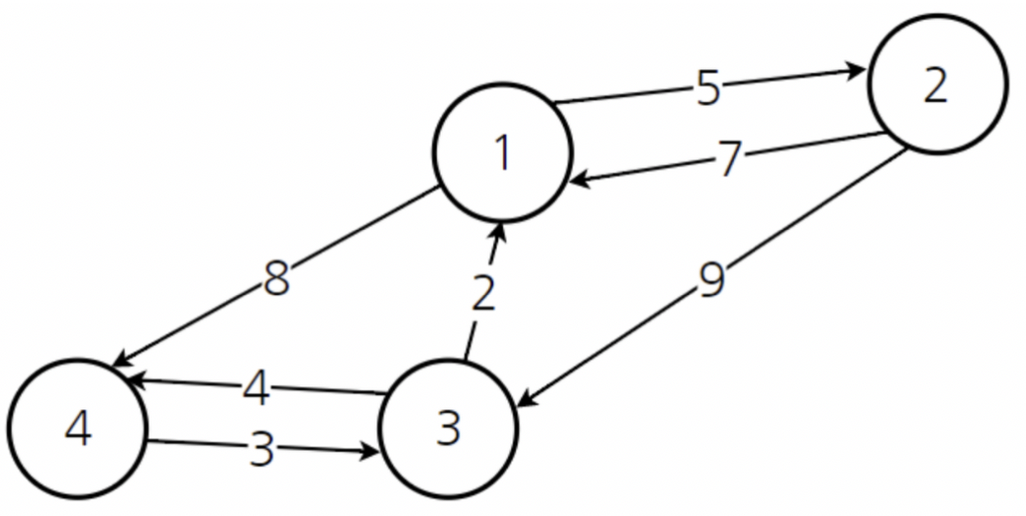
++ +다른 정점으로 가는 비용을 **이차원 배열**로 출력 + +| | 1 | 2 | 3 | 4 | +| --- | --- | --- | --- | --- | +| 1 | 0 | 5 | inf | 8 | +| 2 | 7 | 0 | 9 | inf | +| 3 | 2 | inf | 0 | 4 | +| 4 | inf | inf | 3 | 0 | + +
+ +<****플로이드 와샬(Floyd Warshall)**** 알고리즘을 통해 모든 정점에서 다른 모든 정점의 최단 경로를 구해보기> + +1) 노드 1 을 경유점으로 거쳐가는 경우 + +| | 1 | 2 | 3 | 4 | +| --- | --- | --- | --- | --- | +| 1 | 0 | 5 | inf | 8 | +| 2 | 7 | 0 | 9 | 15 | +| 3 | 2 | 7 | 0 | 4 | +| 4 | inf | inf | 3 | 0 | + +2) 노드 2를 경유점으로 거쳐가는 경우 + +| | 1 | 2 | 3 | 4 | +| --- | --- | --- | --- | --- | +| 1 | 0 | 5 | 14 | 8 | +| 2 | 7 | 0 | 9 | 15 | +| 3 | 2 | 7 | 0 | 4 | +| 4 | inf | inf | 3 | 0 | + +3) 위와 같은 방식으로 노드3, 노드4도 수행해주면 최종적으로 아래와 같은 결과가 나오게 된다 + +| | 1 | 2 | 3 | 4 | +| --- | --- | --- | --- | --- | +| 1 | 0 | 5 | 11 | 8 | +| 2 | 7 | 0 | 9 | 13 | +| 3 | 2 | 7 | 0 | 4 | +| 4 | 5 | 10 | 3 | 0 | + +
+ +## ****플로이드 와샬(Floyd Warshall) 알고리즘 구현**** + +위의 과정들을 보면 경유점을 지나는 최단 거리는 다음과 같이 구할 수 있다. + +C(u, v)는 0번 정점부터 k번 정점까지만을 경유점으로 썼을 때 u에서 v까지 가는 최단 경로의 길이가 된다. + +>⇒ 이 점화식에서 Ck의 모든 값은 Ck-1에만 의존하기 때문에 반복 DP로 쉽게 풀 수 있다. 이렇게 구현한 플로이드 와샬 알고리즘은 3중 for문을 사용하기 때문에 O(V^3)이 된다. + +```java +public class FloydWarshall { + public static void main(String[] args) { + int[][] a = {{1,2,5}, {2,1,7},{3,1,2},{1,4,8},{2,3,9}, + {3,4,3}, {4,3,3}}; + int n =4; + solution(n,a); + } + + static void solution(int n, int[][] arr) { + int[][] floyd = new int[n][n]; + + // 결과 그래프 초기화 + for(int i=0; i
+ +플로이드 와샬 알고리즘은 시간 복잡도가 매우 높기 때문에 효율적인 코드 작성이 필요할 때(코테)는 V의 크기가 크다(500 이상)면 가급적 피하는 것이 좋다. + +그 대신 다익스트라나 다른 방법을 이용해서 더 효율적인 코드를 작성해야 한다.
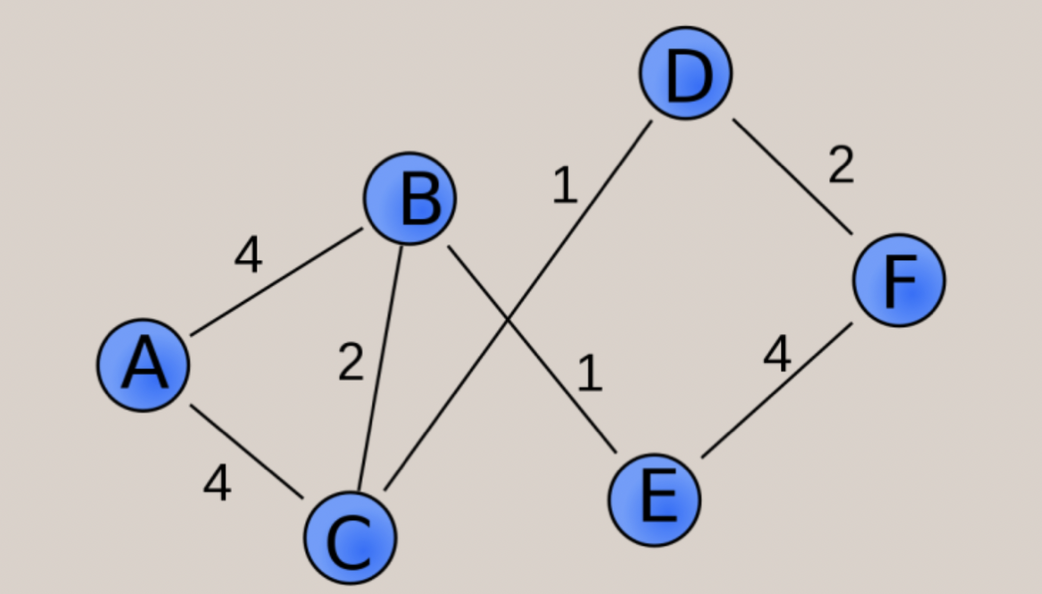 +
+그래프의 간선에 가중치가 있는 그래프
+
+가중치 그래프는 다음과 같이 표현된다.
+
+G = (V,E, w)
+
+- V(G) : 그래프 G의 정점 집합
+- E(G) : 그래프 G의 간선 집합
+- w(e) : 간선 e의 가중치
+
+(간선의 가중치(weight) 또는 비용(cost) 모두 같은 의미이다.)
+
+가중치 그래치 그래프의 응용 분야는 매우 다양한데, 그 중에서 네트워크를 표현하는데 많이 사용되기 때문에 가중치 그래프를 네트워크라고도 한다.
+
+가중치 그래프는 최소 환승, 최단 경로, 최소 비용 등과 같은 것들을 계산할 때 중요하게 활용될 수 있다.
+
+총 비용 = 경로상 존재하는 **간선의 가중치의 총합**
+
+가중치 그래프의 표현은 그래프와 마찬가지로 **인접 행렬, 인접 리스트로 표현**될 수 있다.
+
+
+
+그래프의 간선에 가중치가 있는 그래프
+
+가중치 그래프는 다음과 같이 표현된다.
+
+G = (V,E, w)
+
+- V(G) : 그래프 G의 정점 집합
+- E(G) : 그래프 G의 간선 집합
+- w(e) : 간선 e의 가중치
+
+(간선의 가중치(weight) 또는 비용(cost) 모두 같은 의미이다.)
+
+가중치 그래치 그래프의 응용 분야는 매우 다양한데, 그 중에서 네트워크를 표현하는데 많이 사용되기 때문에 가중치 그래프를 네트워크라고도 한다.
+
+가중치 그래프는 최소 환승, 최단 경로, 최소 비용 등과 같은 것들을 계산할 때 중요하게 활용될 수 있다.
+
+총 비용 = 경로상 존재하는 **간선의 가중치의 총합**
+
+가중치 그래프의 표현은 그래프와 마찬가지로 **인접 행렬, 인접 리스트로 표현**될 수 있다.
+
+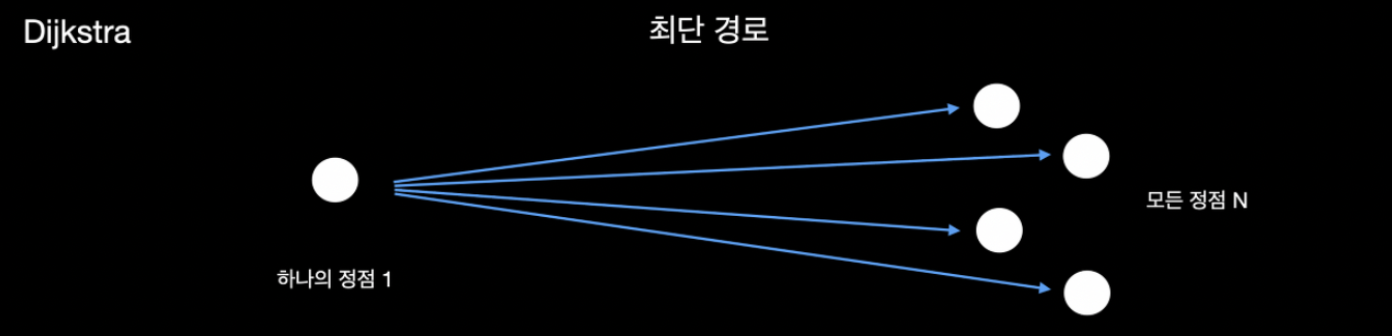 +
+- 다익스트라의 최단 경로 알고리즘은 가장 유명한 그래프 알고리즘 중 하나이며, 단일 시작점 최단 경로 알고리즘으로, 시작 정점 s에서부터 다른 정점들 까지의 최단 거리를 계산한다.
+- DP를 활용한 최단경로 탐색 알고리즘으로 흔히 인공위성 GPS 소프트웨어에서 가장 많이 사용된다.
+- **Dijkstra 알고리즘**은 **하나의 정점**에서 출발했을 때 **다른 모든 정점**으로의 최단 경로를 구하는 알고리즘이다.
+- Dijkstra 알고리즘은 매번 가장 적은 비용을 가진 노드를 하나씩 꺼낸 다음 그 노드를 거쳐가는 비용, 즉 **가장 적은 비용을 하나씩 선택**하는 로직으로 구성 된다.
+
+
+
+- 다익스트라의 최단 경로 알고리즘은 가장 유명한 그래프 알고리즘 중 하나이며, 단일 시작점 최단 경로 알고리즘으로, 시작 정점 s에서부터 다른 정점들 까지의 최단 거리를 계산한다.
+- DP를 활용한 최단경로 탐색 알고리즘으로 흔히 인공위성 GPS 소프트웨어에서 가장 많이 사용된다.
+- **Dijkstra 알고리즘**은 **하나의 정점**에서 출발했을 때 **다른 모든 정점**으로의 최단 경로를 구하는 알고리즘이다.
+- Dijkstra 알고리즘은 매번 가장 적은 비용을 가진 노드를 하나씩 꺼낸 다음 그 노드를 거쳐가는 비용, 즉 **가장 적은 비용을 하나씩 선택**하는 로직으로 구성 된다.
+
+