diff --git a/09/JiYongKim/Tree.md b/09/JiYongKim/Tree.md
new file mode 100644
index 00000000..b0d7d477
--- /dev/null
+++ b/09/JiYongKim/Tree.md
@@ -0,0 +1,178 @@
+### 비선형 구조 자료구조
+
+- 트리
+
+ **트리(Tree) .. (비선형 자료구조)**
+
+ 
+
+ 트리는 노드들이 나무 가지 처럼 연결된 비선형 계층적 자료구조이다.
+
+ - 트리는 트리내에 다른 하위 트리가 있고 그 하위 트리안에 다른 하위 트리가 있는 재귀적 자료구조 이기도 하다.
+ - 컴퓨터 구조가 트리의 대표적인 예시이다.
+
+ 
+
+ - 트리구조 용어
+
+ 
+
+
+ 트리 용어
+
+ - Node
+ - 트리를 구성하고 있는 기본 요소
+ - 노드에는 키 또는 값과 하위 노드에 대한 포인터를 가진다.
+ - Edge
+ - 노드와 노드 간의 연결선
+ - Root Node
+ - 트리 구조에서 부모가 없는 최상위 노드
+ - Parent Node
+ - 자식 노드를 가진 노드
+ - Child Node
+ - 부모 노드의 하위 노드
+ - Sibling Node
+ - 같은 부모를 가지는 노드
+ - Branch Node
+ - 자식 노드가 하나 이상 가진 노드
+ - Leaf Node
+ - 자식 노드가 없는 노드
+ - depth
+ - 루트에서 어떤 노드까지의 간선의 수
+ - 루트 노드의 깊이 : 0
+ - height
+ - 어떤 노드에서 리프 노드까지 가장 긴 경로의 간선(Edge) 수
+ - Level
+ - 루트에서 어떤 노드까지의 간선(Edge) 수
+ - Degree
+ - 노드의 자식 수
+ - Path
+ - 한 노드에서 다른 한 노드에 이르는 길 사이에 놓여있는 노드들의 순서
+ - Path Length
+ - 해당 경로에 있는 총 노드의 수
+ - Size
+ - 자신을 포함한 자손의 노드 수
+ - Width
+ - 레벨에 있는 노드 수
+ - Breadth
+ - 리프 노드의 수
+ - Distance
+ - 두 노드 사이의 최단 경로에 있는 간선(Edge)의 수
+ - Order
+ - 부모 노드가 가질 수 있는 최대 자식의 수
+
+
+
+
+ - 특징
+ - 하나의 루트 노드와 0개 이상의 하위 트리로 구성되어 된다.
+ - 데이터를 순차적으로 저장하지 않기 때문에 비선형 자료구조 이다.
+ - 트리내에 또 다른 트리가 있는 재귀적 자료구조이다.
+ - 단순 순환(Loop)을 갖지 않고, 연결된 무방향 그래프 구조이다.
+ - 노드 간에 부모 자식 관계를 갖고 있는 계층형 자료구조이며 모든 자식 노드는 하나의 부모 노드만 갖는다.
+ - 노드가 n개인 트리는 항상 n-1개의 간선(edge)을 갖는다.
+
+
+
+ - 트리구조 탐색 방식 3가지
+ - 전위 순회(Pre-Order), 중위 순회(In-order), 후위 순회(Post-order)가 존재
+
+ >⇒ 어떠한 순서로 탐색을 진행할 것인지에 따른 분류
+
+ 
+
+ - 전위는 루트 노드를 첫 번째로 봄. [ 중간 -> 왼쪽 -> 오른쪽 ]
+ - 중위는 루트 노드를 두 번째로 봄. [ 왼쪽 -> 중간 -> 오른쪽 ]
+ - 후위는 루트노드를 세 번째로 봄. [ 왼쪽 -> 오른쪽 -> 중간 ]
+
+
+
+ - 트리 종류
+
+ **트리의 종류 1 : 이진트리 ( binary tree )**
+
+ >⇒ 이름에서 알 수 있듯이 최대 2개의 자식 노드를 가질 수 있는 트리이다.
+
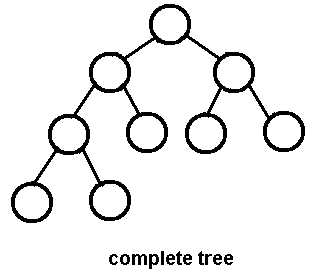
+ 1. 완전 이진트리( complete binary tree )
+
+ - 왼쪽 자식 노드부터 채워지며 마지막 레벨을 제외하고는 모든 자식 노드가 채워져 있는 트리
+
+ 
+
+ - 완전 이진트리를 사용한 힙(Heap) 트리 자료구조.
+ - 여러 개의 값 중에서 가장 크거나 작은 값을 빠르게 찾기 위해 존재.
+ - 우선순위 큐 ( PriorityQueue )에 활용되는 개념.
+ - 부모의 값은 항상 자식의 값보다 크거나(Max heap 최대 힙), 작아야(Min heap) 함
+
+ >⇒ 따라서 루트에는 가장 크거나 작은 값이 저장되어있음.
+
+
+
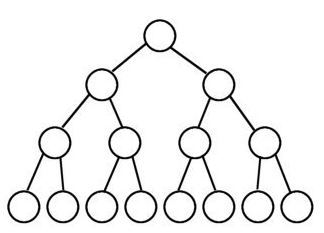
+ 1. 포화 이진트리 ( perfect binary tree )
+
+ - 모든 노드가 0개 혹은 2개의 자식 노드를 가짐.
+ - 모든 리프 노드가 똑같은 레벨에 있는 경우의 트리.
+
+ 
+
+
+
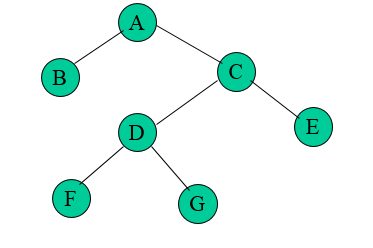
+ 1. 정 이진트리 ( full binary tree )
+
+ - 모든 노드가 0개 혹은 2개의 자식 노드를 가지는 트리
+ - 포화 이진트리의 하위 종류.
+
+ 
+
+
+
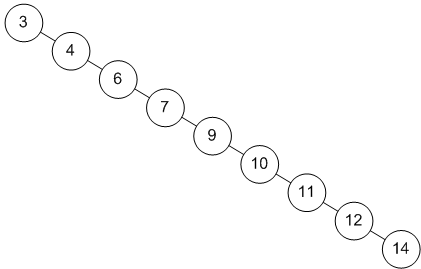
+ 1. 편향 이진트리 ( skwed binary tree )
+
+ - 노드들이 전부 한 방향으로 편향된 트리
+
+ 
+
+
+
+
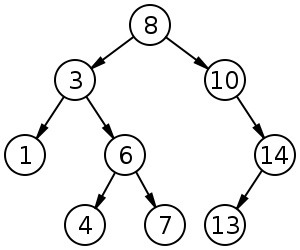
+ 1. 이진 탐색 트리 ( binary search tree )
+ - 이진트리의 종류중 하나
+ - 중요하기 때문에 따로 정리.
+ - 왼쪽 자식 노드가 루트보다 작고, 오른쪽 자식 노드가 루트보다 큰 트리.
+
+ 
+
+ - 여기서 중위 순회하면 오름차순 정렬이 된다.
+
+
+
+ - 트리 사용 사례
+
+ 계층 적 데이터 저장
+
+ - 트리는 데이터를 계층 구조로 저장하는 데 사용됩니다.
+ - 예를 들어 파일 및 폴더는 계층적 트리 형태로 저장됩니다.
+
+
+
+ 효율적인 검색 속도
+
+ - 효율적인 삽입, 삭제 및 검색을 위해 트리 구조를 사용합니다.
+
+
+ 힙(Heap)
+
+ - 힙도 트리로 된 자료 구조입니다.
+
+
+
+ 데이터 베이스 인덱싱
+
+ - 데이터베이스 인덱싱을 구현하는데 트리를 사용합니다.
+ - 예) B-Tree, B+Tree, AVL-Tree..
+
+
+
+ Trie
+
+ - 사전을 저장하는 데 사용되는 특별한 종류의 트리입니다
\ No newline at end of file